在本文中，我将从技术和反思的角度，分享 Spleeft 算法最新优化背后的学习和开发过程。我将解释四年前开发的原始系统的工作原理，以及我在过去一个月中如何对其参数进行微调，以提高准确性和处理速度。
立即下载适用于 iOS、Android 和 Apple Watch 的 SPLEEFT 应用程序！
该算法如何工作？
Spleeft 算法通过积分加速度数据来测量垂直速度。向心阶段通过最小速度阈值来检测，以标记重复动作的开始和结束，并且需要 0.3 米/秒的最小峰值速度来验证动作。此阶段定义最清晰且可预测，因此可以制定更精确的检测规则。
为了检测静止相（这对于校正积分累积的漂移至关重要），我使用了来自惯性传感器的数据：加速度计、陀螺仪和重力。当这些传感器的数值在特定时间窗口内保持在特定阈值以下时，该相位被视为静止。
这种方法论与后来 Achermann等人. 在他们的 Apple Watch 测量杠铃速度的验证研究.
背景和技术背景
在 科学文献传统上，加速度计的速度测量精度被认为低于其他技术。对比研究表明，像 Beast Sensor 或 Push Band 这样的设备精度低于其他解决方案。
然而，加速度计是迄今为止最容易使用的传感器，因为它们被集成到智能手表和可穿戴设备等广泛使用的消费设备中。尽管它们在心率等指标方面的可靠性也受到质疑，但它们在普及基于速度的训练 (VBT) 方面的潜力是不可否认的。
值得注意的是，大多数比较研究评估的是完整系统（硬件 + 软件），而没有区分这两个组件。我认为，将精度低下完全归咎于硬件是不公平的。加速度计如果与专门针对所分析运动类型设计的优化软件配合使用，可以提供精确的结果。因此，在排除一项技术之前，我们必须充分探索其提供的算法可能性。
已有足够证据支持使用 IMU（惯性测量单元）估算升力速度。Enode 或 Output 等公司已经开发出可实现高精度的专有算法。以 Apple Watch 为例，尽管使用了与我不同的算法，但多项研究已验证了其硬件是否适用于此应用。这强化了这样一种观点：合适的算法可以克服通常仅归因于硬件的限制。
IMU 测量速度的局限性
这些限制是一环套一环地出现的。第一个挑战是找到处理惯性传感器数据（加速度计、陀螺仪和磁力计）的最佳方法，以准确估算杆的垂直速度。
主要问题之一是加速度的积分。当使用梯形法（因其简单而广泛使用）进行积分时，系统误差（称为 漂移 随着时间的推移，漂移会逐渐积累。为了弥补这一点，有必要识别已知的零速度矩（称为静止相），以便进行漂移校正。
用于估计垂直速度的信号处理
惯性传感器提供三个空间轴的数据。然而，直接使用加速度计的垂直分量是不够的，因为单凭这个传感器无法精确确定测量力的方向。为了解决这个问题，我使用了卡尔曼、马奥尼和马德威克等传感器融合算法，这些算法提供方向四元数来校正设备的参考系。
我使用不同的方向算法处理了来自 Apple Watch 和 iPhone 的数据，并将其与运动捕捉系统（STT Systems）进行了比较。我选择了在移动设备上实现准确性和计算效率之间最佳平衡的组合。
方向校正后，加速度积分即可得到速度。为了进一步减少漂移，我测试了低通滤波器的使用，例如 巴特沃斯滤波器，在生物力学中有着广泛的应用。
零速更新（ZUPT）
在测试过程中，我发现主要问题并非取向校正或积分本身，而是应用ZUPT所需的固定相检测。这些固定相必须快速可靠地检测，因为它们的准确性直接影响系统的精度。
没有单一的方法可以实现这一点。因此，我开发了一种基于多参数组合系统分析的经验方法：使用哪些传感器、应用哪些阈值以及考虑哪些时间窗口。
利用数据科学进行算法优化
定义好所有变量后，我在实验室收集了大量健身房训练重复次数的数据集，并存储了原始传感器数据。同时，我使用了一个黄金标准系统进行比较。所选的训练动作包括：反弹深蹲、暂停硬拉（包括向心和离心）以及高位下拉。所有组别都以高强度进行，以适应不同的疲劳程度，并在每次训练之间尽量减少休息时间。
这种设置允许我优化算法的准确性和速度，即使在重复之间几乎没有或没有静止相的情况下也是如此 - 这是基于集成的方法最具挑战性的情况。
我创建了一个 Python 脚本来系统地探索 13,486 个参数组合：
- 是否应用低通滤波器，以及截止频率。
- ZUPT 参数：阈值、时间窗口和传感器组合。
- 同心检测的最小速度阈值。
在运行完整数据集（耗时数小时）后，我根据运动类型、速度范围和停止类型分别分析了表现最佳的组合。我的目标不仅是找到性能最佳的配置，更是为了更好地理解系统的行为，以便日后改进。
现场测试
在实际验证过程中，我发现主要的瓶颈在于算法在检测稳定相时的延迟。用户反馈很明确：系统反馈时间太长了。
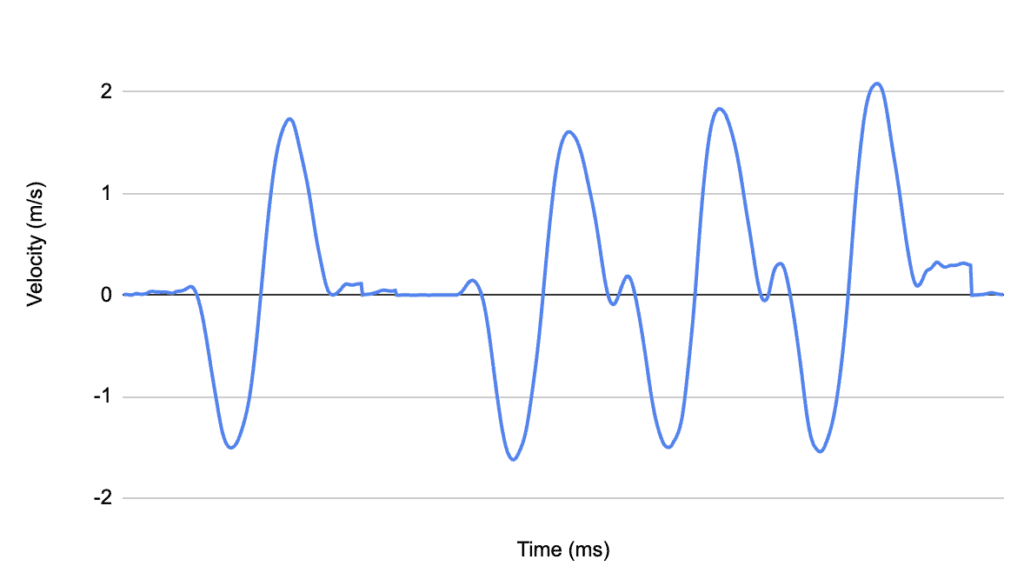
在查看许多速度-时间图时，我注意到 第一次重复即使没有应用 ZUPT，也几乎没有漂移。这是因为漂移会随着时间的推移而增长。我问自己：累积的漂移是否足够大，足以对平均速度估计产生显著影响？
为了回答这个问题，我测试了在向心阶段之前先进行大量离心阶段的深蹲。我等待第一个静止阶段来校准系统，然后连续进行不间断的重复训练。结果令人惊讶：平均误差仅为 0.018米/秒，甚至更低（0.016米/秒) 在最新的验证中。与校正值相比，差异很小，但响应时间显著改善，从 800 毫秒缩短至 200 毫秒。这使得反馈能够传递 紧接着 向心阶段，而不是几秒钟后。
尽管如此，ZUPT 算法仍然有效。当检测到新的固定相时，系统会重新校准信号，并校正任何累积的误差。如果在固定相之间重复测量超过一次，则校正值将覆盖初始反馈，以确保用户始终获得最准确的结果。
结论
这个数据驱动的项目让我能够显著优化 Spleeft 算法。我成功地缩短了平均速度估算的响应时间，同时又不损害之前验证的可靠性。关键在于将系统的数据收集与全面的参数探索相结合——要明白最终结果的质量不仅取决于硬件，甚至可能更多地取决于其背后的软件。
